Berechnung von DGA Trends - Offline vs. Online
Transformatorentechnologie neu definiert
Die Analyse gelöster Gase (dissolved gas analysis = DGA) ist eine der besten Methoden zur Zustandsschätzung von Transformatoren, aber die Interpretation von DGA-Ergebnissen ist nach wie vor ein aktives Forschungsfeld. Die Analyse von Trends (oder Steigerungsraten) ist ein wichtiger Bestandteil der modernen DGA-Analyse. Mithilfe von Trends können Ausfälle früher erkannt und die Häufigkeit von Fehlalarmen verringert werden.
Bevor jedoch eine Interpretation vorgenommen werden kann, muss der tatsächliche Trendwert (in ppm/Tag oder ppm/Jahr) berechnet werden. Das ist leichter gesagt als getan. Die IEEE-Norm C57.104 gibt einige Hinweise, wie dies bei Offline-Messungen (im Labor) zu bewerkstelligen ist. Online-Trends (Überwachung) werden aufgrund der größeren Häufigkeit der verfügbaren Daten anders berechnet.
Dieser Artikel versucht, einen ersten Überblick über die DGA-Trendberechnung sowohl für Offline- als auch für Online-Messungen zu geben.

Offline-DGA
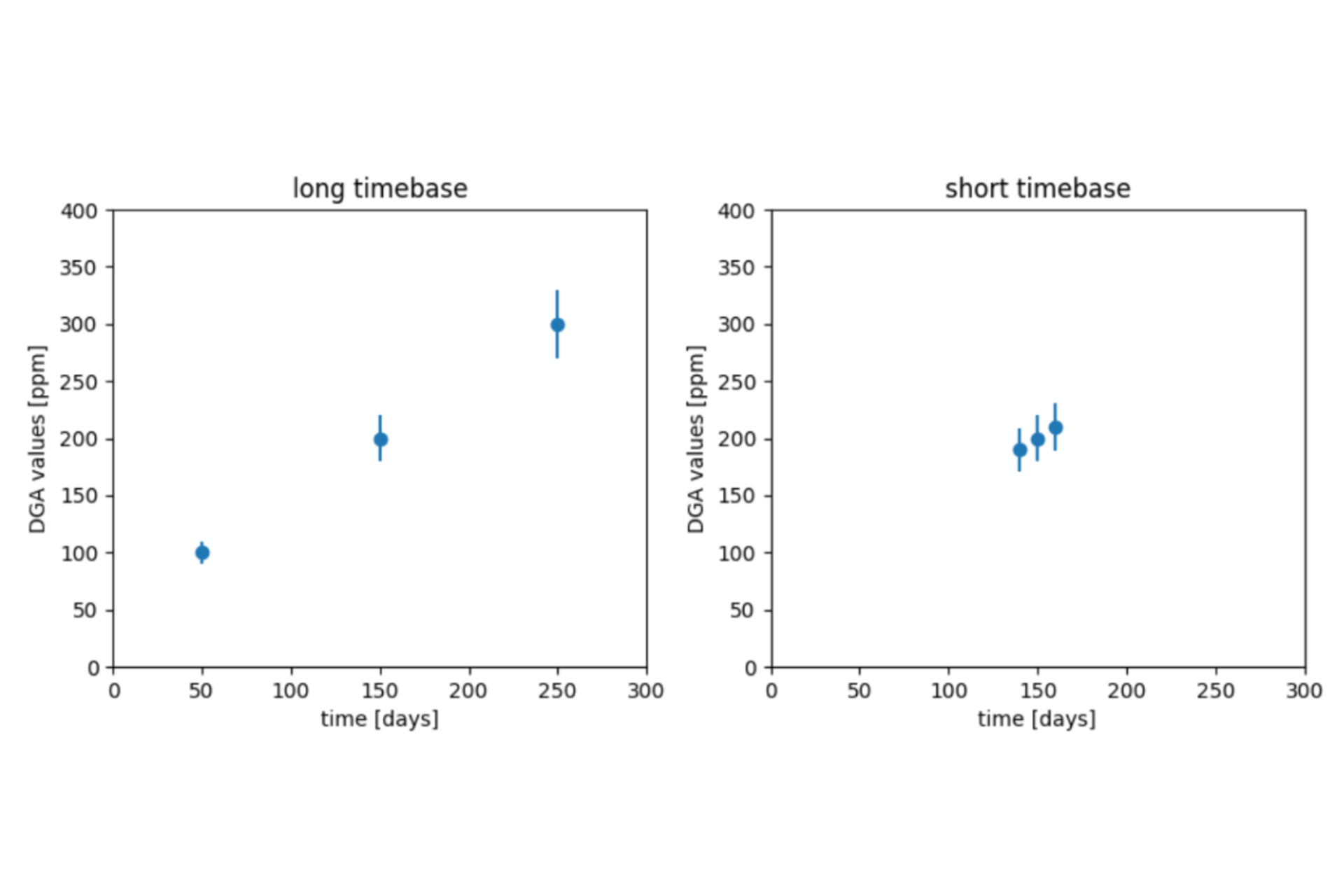
Ein Trend kann mathematisch definiert werden als die Wachstumsrate - Wertedifferenz geteilt durch Zeitdifferenz. Diese Definition wäre für uns ausreichend, wenn der Trend konstant ist und keine Messunsicherheit besteht. Diese Bedingungen sind im Zusammenhang mit der DGA-Analyse in der Regel nicht erfüllt. Zur Veranschaulichung wollen wir zwei Beispiele betrachten. Im ersten Beispiel (lange Zeitbasis) werden die Messungen im Abstand von 100 Tagen vorgenommen. Im zweiten Beispiel (kurze Zeitbasis) werden die Messungen im Abstand von 10 Tagen durchgeführt. Beide Beispiele haben eine Messunsicherheit von 10% und einen tatsächlichen Trend von 1 ppm pro Tag. Dies ist in der nebenstehenden Abbildung dargestellt.
Unter Berücksichtigung der Unsicherheit ist es offensichtlich, dass ein aus dem Beispiel mit langer Zeitbasis berechneter Trend robuster ist als der andere. Die Unsicherheitssbereiche auf dem Diagramm mit kurzer Zeitbasis wären theoretisch sogar mit einem negativen Trend kompatibel.
Daher ist es wichtig, bei der Interpretation der berechneten Trends die Zeitbasis im Auge zu behalten. Längere Zeiträume ergeben zuverlässigere Trends, aber das hat seinen Preis: Wenn längere Zeiträume verwendet werden, steigen die berechneten Trends langsamer und Fehler werden später erkannt.
Dieser Effekt steht auch in Wechselwirkung mit der Anzahl der zur Berechnung eines Trends verwendeten Datenpunkte. Wenn weniger Datenpunkte verwendet werden, hat die Unsicherheit jedes Punktes einen größeren Einfluss. Wenn mehr Datenpunkte verwendet werden, ist es wahrscheinlich, dass ein Teil des Rauschens ausgelöscht wird. Mehr Datenpunkte können durch Erhöhung der Messhäufigkeit oder durch Vergrößerung der Zeitspanne gewonnen werden.
Ein Trend kann immer dann durch das Zeichnen einer Linie berechnet werden, wenn nur zwei Datenpunkte verfügbar sind, aber es ist unwahrscheinlich, dass 3 oder mehr Punkte auf einer Linie liegen. Zur Berechnung des Trends für 3 oder mehr Punkte empfiehlt die oben genannte Norm die Verwendung eines Tabellenkalkulationsprogramms zur Berechnung der "linearen Mehrpunktanpassung" - ein anderer Begriff für lineare Regression. Wenn Unsicherheitsinformationen für jede Probe verfügbar sind, kann eine lineare Bayessche Regressionsanalyse verwendet werden, um diese Informationen zu berücksichtigen.
Die Erkennung von Ausreißern kann der Regressionsanalyse vorausgehen, um zu verhindern, dass Ausreißer einen unzulässigen Einfluss haben. Eine einfache Möglichkeit hierfür ist die Verwendung eines Hampelfilters, der allerdings den Nachteil hat, dass Ausreißer in den letzten beiden Messungen nicht erkannt werden können. Alternativ kann eine robuste Regressionsanalyse die Aufgaben der Ausreißererkennung und der Trendberechnung kombinieren. Wenn eine Bayessche Regressionsanalyse verwendet wird, kann ein robustes Regressionsverhalten durch die Annahme von fat-failed Verteilungen im Rauschterm erreicht werden.
Natürlich gibt es nicht den einen besten Weg, dies zu tun. Die IEEE-Norm C57.104 empfiehlt die Verwendung einer einfachen linearen Regression mit 3 bis 6 Datenpunkten und einer Zeitbasis von 4 bis 24 Monaten, wobei die jüngsten 6 Datenpunkte verwendet werden, falls mehr verfügbar sind. Dies führt zu einem ausgewogenen Verhältnis von Reaktionszeit, Einfachheit und Genauigkeit, das für viele Situationen geeignet sein sollte.
Praktischer Nebeneffekt: Wenn ein Transformator jährlich im Labor geprüft wird, werden immer mindestens 3 Datenpunkte für die Zeitspanne von 24 Monaten direkt nach der letzten Messung verfügbar sein. 365 Tage zwischen den Messungen dürfen aber nie überschritten werden, und Ausreißer dürfen nicht auftreten, damit dieses Schema funktioniert.
Online-DGA
DGA-Monitore erzeugen mehrere Datenpunkte pro Tag. Dies steht in krassem Gegensatz zu Offline-Messungen, bei denen wir froh sein können, wenn es mehrere Datenpunkte pro Jahr gibt. Die relative Fülle an Daten führt zu schnelleren Reaktionszeiten und einem besseren Umgang mit Ausreißern. Außerdem verbessert die automatisierte Art und Weise, in der die Messungen erstellt werden, die Reproduzierbarkeit der Daten. Dies ist besonders für die Trendanalyse hilfreich.
Die eigentliche Berechnung dieses Trends kann immer noch mit einer Regressionsanalyse erfolgen. Dabei werden in der Regel nur die neuesten Messungen in die Analyse einbezogen, so dass sich Trends beispielsweise über die letzten 30 Tage ergeben. Da in diesem Zeitraum viele Datenpunkte verfügbar sind, kann auch eine Ausreißeranalyse durchgeführt werden, die den Einfluss von Ausreißern noch weiter reduziert.
Zusammengefasst:
Das hört sich nach viel Mathematik an, aber zum Glück müssen wir das nicht manuell machen. Der DGA-Online-Monitor übernimmt diese Aufgabe für uns.
